Динамическая политика
Динамическая политика обеспечивает вероятностные гарантии согласованности за счет регулировки порогового значения.
Модель. Как и при рассмотрении Общей политики, мы предполагаем, что имеется интервал кэширования, и что обновления равномерно распределены между серверами. Следовательно, вероятность того, что значение некоторой записи станет отрицательно, выражается следующим образом:
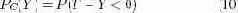
Здесь Y – это случайная переменная, соответствующая общему объему изменений в течение интервала кэширования CI. Y отличается от X из соотношения (1) тем, что в значении этой переменной отражается не число выполненных операций обновления, а общий объем всех обновлений в течение интервала кэширования. P(T - Y < 0) соответствует вероятности нарушения ограничения согласованности (например, за счет покупки слишком большого числа товаров до того, как сервер начинает применять строгую согласованность).
Темпоральная статистика. Для сбора статистики для Y мы снова используем окно с размеров w и показателем скольжения δ. В отличие от случая Общей политики, мы полагаем, что показатель скольжения δ не кратен интервалу кэширования CI, а является его долей. Для этого имеются два основания. Во-первых, для Динамической политики требуется определение дисперсии. Более точные значения дисперсии получаются при использовании меньших показателей скольжения. Во-вторых, политика концентрируется на часто обновляемых значениях. События (т.е. обновления) не являются редкими, и, следовательно, требуемый объем данных можно собрать в течение меньшего времени.
Для каждого интервала скольжения собирается общий объем всех обновлений данных категории B. Все завершившиеся интервалы окна составляют гистограмму обновлений. Если в некоторой транзакции требуется обновить некоторую запись, то на основе гистограммы скользящего окна с использованием стандартной формулы вычисляется эмпирическая функция плотности вероятности (probability density function, PDF) f. Затем f свертывается (convoluted) CI / δ раз для построения PDF fCI для всего интервала кэширования:
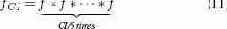
Свертка требуется, поскольку для нас важно сохранить десперсию.
Чтобы можно было судить об обновлениях в системе целиком, должно быть известно число серверов n. Если свернуть n раз fCI, мы получим PDF для обновлений во всей системе:

При наличии fCI*n можно построить интегральную функцию распределения (cumulative distribution function, CDF), которую, в конце концов, можно использовать для определения порогового значения для P(T - X < 0) путем поиска такой вероятности, что

Для оптимизации PC(Y) можно использовать тот же метод, что и ранее:

Заметим, что пороговое значение T определяется при условии, что вероятность больше, чем PC(Y), а не меньше.
Хотя существуют эффективные алгоритмы свертки функций, если значение n*CI/δ достаточно велико и/или элемент часто обновляется, то центральная предельная теорема позволяет аппроксимировать CDF нормальным распределением. Это обеспечивает возможность более быстрого вычисления порогового значения для гарантирования процентиля согласованности. С использованием гистограммы плавающего окна можно вычислить арифметическое среднее значение

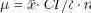
и стандартным отклонением
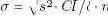
Мы используем статистические данные собираемые во время выполнения, для установки порогового значения для каждой отдельной записи в зависимости от частоты ее обновления. Как показывают результаты эксперимента 2, описываемые в разд. 7, это Динамическая политика превосходит все другие политики по показателям как производительности, так и стоимости. Поскольку статистика собирается во время выполнения, система также имеет возможность реагировать на изменение темпа поступления операций изменения записей.
